RandomLib::DiscreteNormalAlt< IntType, bits > Class Template Reference

The discrete normal distribution (alternate version). More...

#include <RandomLib/DiscreteNormalAlt.hpp>

Public Member Functions
	DiscreteNormalAlt (IntType sigma_num, IntType sigma_den=1, IntType mu_num=0, IntType mu_den=1)
template<class Random >
UniformInteger< IntType, bits >	operator() (Random &r) const

Detailed Description

template<typename IntType = int, int bits = 1>
class RandomLib::DiscreteNormalAlt< IntType, bits >

The discrete normal distribution (alternate version).

Sample integers i with probability proportional to

\[ \exp\biggl[-\frac12\biggl(\frac{i-\mu}{\sigma}\biggr)^2\biggr], \]

where σ and μ are given as rationals (the ratio of two integers). The sampling is exact (provided that the random generator is ideal). The results of this class are UniformInteger objects which represent a contiguous range which is a power of 2^bits. This can be narrowed down to a specific integer as follows

#include <iostream>
#include <RandomLib/Random.hpp>
#include <RandomLib/UniformInteger.hpp>
#include <RandomLib/DiscreteNormalAlt.hpp>

int main() {
  RandomLib::Random r;          // Create r
  r.Reseed();                   // and give it a unique seed
  int sigma_num = 7, sigma_den = 1, mu_num = 1, mu_den = 3;
  RandomLib::DiscreteNormalAlt<int,1> d(sigma_num, sigma_den,
                                        mu_num, mu_den);
  for (int i = 0; i < 100; ++i) {
    RandomLib::UniformInteger<int,1> u = d(r);
    std::cout << u << " = ";
    std::cout << u(r) << "\n";
  }
}

prints out 100 samples with σ = 7 and μ = 1/3; the samples are first given as a range and then u(r) is used to obtain a specific integer. In some applications, it might be possible to avoid sampling all the additional digits to get to a specific integer. (An example would be drawing a sample which satisfies an inequality.) This version is slower (by a factor of about 4 for bits = 1) than DiscreteNormal on a conventional computer, but may be faster when random bits are generated by a slow hardware device.

The basic algorithm is the same as for DiscreteNormal. However randomness in metered out bits random bits at a time. The algorithm uses the least random bits (and is slowest!) when bits = 1. This rationing of random bits also applies to sampling j in the expression

\[ x = x_0 + j/\sigma. \]

Rather than sampling a definite value for j, which then might be rejected, j is sampled using UniformInteger. UniformInteger uses Lumbroso's method from sampling an integer uniformly in [0, m) using at most 2 + log₂m bits on average (for bits = 1). However when a UniformInteger object is first constructed it samples at most 3 bits (on average) to obtain a range for j which is power of 2. This allows the algorithm to achieve ideal scaling in the limit of large σ consuming constant + log₂σ bits on average. In addition it can deliver the resuls in the form of a UniformInteger consuming a constant number of bits on average (and then about log₂σ additional bits are required to convert the UniformInteger into an integer sample). The consumption of random bits (for bits = 1) is summarized here

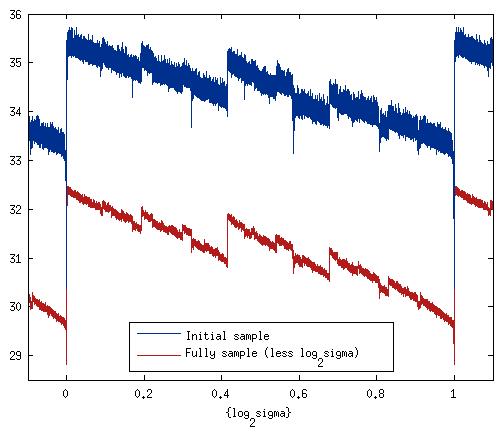
                                          min   mean  max
  bits for UniformInteger result          30.4  34.3  35.7
  bits for integer result - log2(sigma)   28.8  31.2  32.5
  toll                                    26.8  29.1  30.4 

These results are averaged over many samples. The "min" results apply when σ is a power of 2; the "max" results apply when σ is slightly more than a power of two; the "mean" results are averaged over σ. The toll is the excess number of bits over the entropy of the distribution, which is log₂(2πe)/2 + log₂σ (for σ large).

The data for the first two lines in the table above are taken for the blue and red lines in the figure below where the abscissa is the fractional part of log₂σ

Random bits to sample from discrete normal distribution

This class uses a mutable RandomNumber objects. So a single DiscreteNormalAlt object cannot safely be used by multiple threads. In a multi-processing environment, each thread should use a thread-specific DiscreteNormalAlt object.

Template Parameters

IntType

the integer type to use (default int).

Definition at line 104 of file DiscreteNormalAlt.hpp.

Constructor & Destructor Documentation

template<typename IntType , int bits>

RandomLib::DiscreteNormalAlt< IntType, bits >::DiscreteNormalAlt	(	IntType	sigma_num,
		IntType	sigma_den = 1,
		IntType	mu_num = 0,
		IntType	mu_den = 1
	)

Constructor.

Parameters

[in]	sigma_num	the numerator of σ.
[in]	sigma_den	the denominator of σ (default 1).
[in]	mu_num	the numerator of μ (default 0).
[in]	mu_den	the denominator of μ (default 1).

This may throw an exception is the parameters are such that overflow is possible.

Definition at line 179 of file DiscreteNormalAlt.hpp.

References STATIC_ASSERT.

Member Function Documentation

template<typename IntType , int bits>

template<class Random >

UniformInteger< IntType, bits > RandomLib::DiscreteNormalAlt< IntType, bits >::operator()

(

Random &

r

)

const

Return a sample.

Template Parameters

Random

the type of the random generator.

Parameters

[in,out]

r

a random generator.

Returns

discrete normal sample in the form of a UniformInteger object.

Definition at line 230 of file DiscreteNormalAlt.hpp.

References RandomLib::UniformInteger< IntType, bits >::Add(), RandomLib::RandomCanonical< Generator >::Boolean(), RandomLib::UniformInteger< IntType, bits >::GreaterThan(), RandomLib::UniformInteger< IntType, bits >::LessThan(), and RandomLib::UniformInteger< IntType, bits >::Negate().

---

The documentation for this class was generated from the following file:

• DiscreteNormalAlt.hpp