Sample exactly from an exponential distribution. More...

#include <RandomLib/ExactExponential.hpp>

Public Member Functions
template<class Random >
RandomNumber< bits >	operator() (Random &r) const

Detailed Description

template<int bits = 1>
class RandomLib::ExactExponential< bits >

Sample exactly from an exponential distribution.

Sample x ≥ 0 from exp(−x). See:

J. von Neumann, Various Techniques used in Connection with Random Digits, J. Res. Nat. Bur. Stand., Appl. Math. Ser. 12, 36–38 (1951), reprinted in Collected Works, Vol. 5, 768–770 (Pergammon, 1963).
M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions (National Bureau of Standards, 1964), Sec. 26.8.6.c(2).
G. E. Forsythe, Von Neumann's Comparison Method for Random Sampling from Normal and Other Distributions, Math. Comp. 26, 817–826 (1972).
D. E. Knuth, TAOCP, Vol 2, Sec 3.4.1.C.3.
D. E. Knuth and A. C. Yao, The Complexity of Nonuniform Random Number Generation, in "Algorithms and Complexity" (Academic Press, 1976), pp. 357–428.
P. Flajolet and N. Saheb, The Complexity of Generating an Exponentially Distributed Variate, J. Algorithms 7, 463–488 (1986).

The following code illustrates the basic method given by von Neumann:

// Return a random number x >= 0 distributed with probability exp(-x).
double ExpDist(RandomLib::Random& r) {
  for (unsigned k = 0; ; ++k) {
    double x = r.Fixed(),    // executed 1/(1-exp(-1)) times on average
      p = x, q;
    do {
      q = r.Fixed();         // executed exp(x)*cosh(x) times on average
      if (!(q < p)) return k + x;
      p = r.Fixed();         // executed exp(x)*sinh(x) times on average
    } while (p < q);
  }
}

This returns a result consuming exp(1)/(1 − exp(-1)) = 4.30 random numbers on average. (Von Neumann incorrectly states that the method takes (1 + exp(1))/(1 − exp(-1)) = 5.88 random numbers on average.) Because of the finite precision of Random::Fixed(), the code snippet above only approximates exp(−x). Instead, it returns x with probability h(1 − h)^x/h for x = ih, h = 2⁻⁵³, and integer i ≥ 0.

The above is precisely von Neumann's method. Abramowitz and Stegun consider a variant: sample uniform variants until the first is less than the sum of the rest. Forsythe converts the < ranking for the runs to ≤ which makes the analysis of the discrete case more difficult. He also drops the "trick" by which the integer part of the deviate is given by the number of rejections when finding the fractional part.

Von Neumann says of his method: "The machine has in effect computed a logarithm by performing only discriminations on the relative magnitude of numbers in (0,1). It is a sad fact of life, however, that under the particular conditions of the Eniac it was slightly quicker to use a truncated power series for log(1−T) than to carry out all the discriminations."

Here the code is modified to make it more efficient:

// Return a random number x >= 0 distributed with probability exp(-x).
double ExpDist(RandomLib::Random& r) {
  for (unsigned k = 0; ; ++k) {
    double x = r.Fixed();   // executed 1/(1-exp(-1/2)) times on average
    if (x >= 0.5) continue;
    double p = x, q;
    do {
      q = r.Fixed();        // executed exp(x)*cosh(x) times on average
      if (!(q < p)) return 0.5 * k + x;
      p = r.Fixed();        // executed exp(x)*sinh(x) times on average
    } while (p < q);
  }
}

In addition, the method is extended to use infinite precision uniform deviates implemented by RandomNumber and returning exact results for the exponential distribution. This is possible because only comparisons are done in the method. The template parameter bits specifies the number of bits in the base used for RandomNumber (i.e., base = 2^bits).

For example the following samples from an exponential distribution and prints various representations of the result.

#include <RandomLib/RandomNumber.hpp>
#include <RandomLib/ExactExponential.hpp>
  RandomLib::Random r;
  const int bits = 1;
  RandomLib::ExactExponential<bits> edist;
  for (size_t i = 0; i < 10; ++i) {
    RandomLib::RandomNumber<bits> x = edist(r); // Sample
    std::pair<double, double> z = x.Range();
    std::cout << x << " = "     // Print in binary with ellipsis
              << "(" << z.first << "," << z.second << ")"; // Print range
    double v = x.Value<double>(r); // Round exactly to nearest double
    std::cout << " = " << v << "\n";
  }

Here's a possible result:

0.0111... = (0.4375,0.5) = 0.474126
10.000... = (2,2.125) = 2.05196
1.00... = (1,1.25) = 1.05766
0.010... = (0.25,0.375) = 0.318289
10.1... = (2.5,3) = 2.8732
0.0... = (0,0.5) = 0.30753
0.101... = (0.625,0.75) = 0.697654
0.00... = (0,0.25) = 0.0969214
0.0... = (0,0.5) = 0.194053
0.11... = (0.75,1) = 0.867946

First number is in binary with ... indicating an infinite sequence of random bits. Second number gives the corresponding interval. Third number is the result of filling in the missing bits and rounding exactly to the nearest representable double.

This class uses some mutable RandomNumber objects. So a single ExactExponential object cannot safely be used by multiple threads. In a multi-processing environment, each thread should use a thread-specific ExactExponential object. In addition, these should be invoked with thread-specific random generator objects.

Template Parameters

bits	the number of bits in each digit.

Definition at line 145 of file ExactExponential.hpp.

Member Function Documentation

template<int bits>

template<class Random >

RandomNumber< bits > RandomLib::ExactExponential< bits >::operator() ( Random & r ) const

Return a random deviate with an exponential distribution, exp(−x) for x ≥ 0. Requires 7.232 bits per invocation for bits = 1. The average number of bits in the fraction = 1.743. The relative frequency of the results for the fractional part with bits = 1 is shown by the histogram

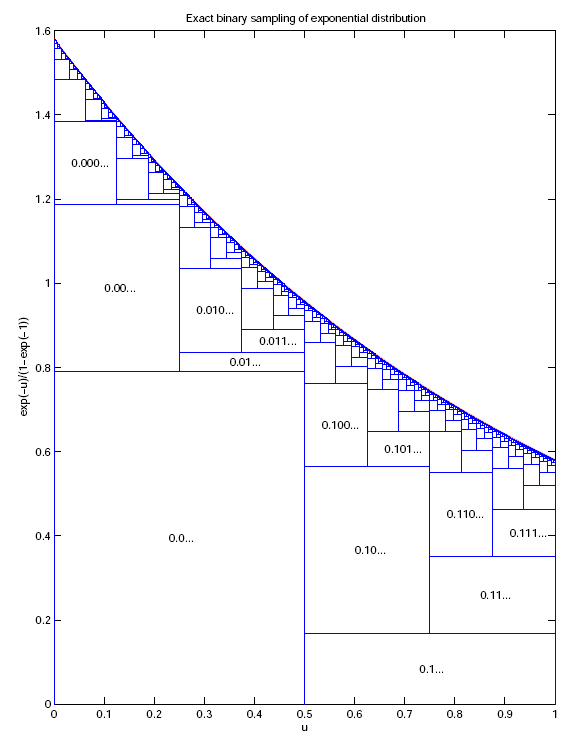
The base of each rectangle gives the range represented by the corresponding binary number and the area is proportional to its frequency. A PDF version of this figure is given here. This allows the figure to be magnified to show the rectangles for all binary numbers up to 9 bits. Note that this histogram was generated using an earlier version of ExactExponential (thru version 1.3) that implements von Neumann's original method. The histogram generated with the current version of ExactExponential is the same as this figure for u in [0, 1/2]. The histogram for u in [1/2, 1] is obtained by shifting and scaling the part for u in [0, 1/2] to fit under the exponential curve.

Another way of assessing the efficiency of the algorithm is thru the mean value of the balance = (number of random bits consumed) − (number of bits in the result). If we code the result in mixed Knuth and Yao's unary-binary notation (integer is given in unary, followed by "0" as a separator, followed by the fraction in binary), then the mean balance is 3.906. (Flajolet and Saheb analyzed the algorithm based on the original von Neumann method and showed that the balance is 5.680 in that case.)

For bits large, the mean number of random digits is exp(1/2)/(1 − exp(−1/2)) = 4.19 (versus 4.30 digits for the original method).

Template Parameters

Random the type of the random generator.

Parameters

[in,out] r a random generator.

Returns: the random sample.

Definition at line 196 of file ExactExponential.hpp.

The documentation for this class was generated from the following file:

ExactExponential.hpp

Public Member Functions

Detailed Description

template<int bits = 1> class RandomLib::ExactExponential< bits >

Member Function Documentation

template<int bits = 1>
class RandomLib::ExactExponential< bits >